Gcf Of 64 And 36

GCF of 36 and 64

GCF of 36 and 64 is the largest possible number that divides 36 and 64 exactly without whatever remainder. The factors of 36 and 64 are ane, 2, 3, iv, 6, nine, 12, eighteen, 36 and i, two, 4, 8, 16, 32, 64 respectively. At that place are 3 usually used methods to find the GCF of 36 and 64 - Euclidean algorithm, prime number factorization, and long division.

one.	GCF of 36 and 64
2.	Listing of Methods
3.	Solved Examples
4.	FAQs

What is GCF of 36 and 64?

Answer: GCF of 36 and 64 is 4.

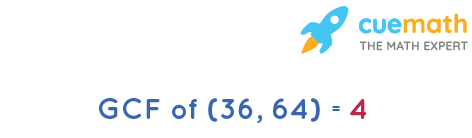
Explanation:

The GCF of two not-nix integers, x(36) and y(64), is the greatest positive integer chiliad(4) that divides both x(36) and y(64) without whatsoever remainder.

Methods to Discover GCF of 36 and 64

The methods to find the GCF of 36 and 64 are explained below.

• Listing Common Factors
• Long Division Method
• Using Euclid's Algorithm

GCF of 36 and 64 by List Common Factors

• Factors of 36: 1, ii, 3, 4, vi, 9, 12, 18, 36
• Factors of 64: 1, 2, 4, 8, sixteen, 32, 64

At that identify are iii common factors of 36 and 64, that are 1, 2, and 4. Therefore, the greatest common cistron of 36 and 64 is iv.

GCF of 36 and 64 past Long Partitioning

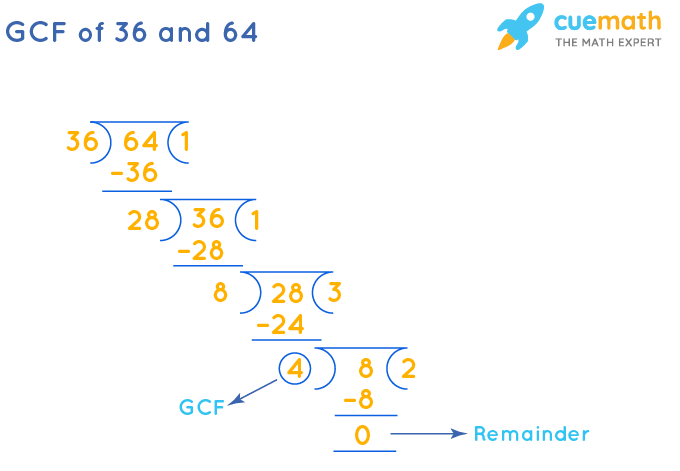
GCF of 36 and 64 is the divisor that nosotros get when the balance becomes 0 afterwards doing long division repeatedly.

• Pace 1: Divide 64 (larger number) by 36 (smaller number).
• Step 2: Since the remainder ≠ 0, nosotros will divide the divisor of stride i (36) past the rest (28).
• Step 3: Repeat this procedure until the remainder = 0.

The respective divisor (4) is the GCF of 36 and 64.

GCF of 36 and 64 by Euclidean Algorithm

Equally per the Euclidean Algorithm, GCF(X, Y) = GCF(Y, X modernistic Y)
where 10 > Y and modernistic is the modulo operator.

Here X = 64 and Y = 36

• GCF(64, 36) = GCF(36, 64 mod 36) = GCF(36, 28)
• GCF(36, 28) = GCF(28, 36 mod 28) = GCF(28, eight)
• GCF(28, 8) = GCF(8, 28 modernistic 8) = GCF(8, four)
• GCF(viii, 4) = GCF(4, viii modernistic four) = GCF(four, 0)
• GCF(4, 0) = four (∵ GCF(10, 0) = |X|, where 10 ≠ 0)

Therefore, the value of GCF of 36 and 64 is iv.

☛ Also Bank check:

• GCF of 30 and 54 = half-dozen
• GCF of xxx and 70 = ten
• GCF of xv and 28 = 1
• GCF of 35 and 63 = seven
• GCF of 32 and 36 = 4
• GCF of 39 and 65 = 13
• GCF of 86 and 42 = 2

GCF of 36 and 64 Examples

1. Instance 1: Detect the GCF of 36 and 64, if their LCM is 576.

   Solution:

   ∵ LCM × GCF = 36 × 64
   ⇒ GCF(36, 64) = (36 × 64)/576 = iv
   Therefore, the greatest common factor of 36 and 64 is 4.

2. Case 2: Notice the greatest number that divides 36 and 64 exactly.

   Solution:

   The greatest number that divides 36 and 64 exactly is their greatest common factor, i.east. GCF of 36 and 64.
   ⇒ Factors of 36 and 64:

   • Factors of 36 = ane, two, three, four, 6, 9, 12, 18, 36
   • Factors of 64 = 1, ii, iv, 8, sixteen, 32, 64

   Therefore, the GCF of 36 and 64 is 4.

3. Instance 3: For ii numbers, GCF = 4 and LCM = 576. If i number is 64, find the other number.

   Solution:

   Given: GCF (x, 64) = four and LCM (ten, 64) = 576
   ∵ GCF × LCM = 64 × (10)
   ⇒ ten = (GCF × LCM)/64
   ⇒ 10 = (4 × 576)/64
   ⇒ x = 36
   Therefore, the other number is 36.

become to slidego to slidego to slide

Set to see the world through math'due south eyes?

Math is at the cadre of everything we practice. Bask solving real-world math bug in live classes and go an good at everything.

Volume a Complimentary Trial Form

FAQs on GCF of 36 and 64

What is the GCF of 36 and 64?

The GCF of 36 and 64 is 4 . To summate the greatest mutual factor (GCF) of 36 and 64, we need to factor each number (factors of 36 = one, two, 3, four, half-dozen, 9, 12, eighteen, 36; factors of 64 = 1, 2, four, eight, 16, 32, 64) and choose the greatest cistron that exactly divides both 36 and 64, i.east., 4.

If the GCF of 64 and 36 is 4, Detect its LCM.

GCF(64, 36) × LCM(64, 36) = 64 × 36
Since the GCF of 64 and 36 = iv
⇒ 4 × LCM(64, 36) = 2304
Therefore, LCM = 576
☛ GCF Estimator

What is the Relation Betwixt LCM and GCF of 36, 64?

The following equation tin exist used to express the relation between Least Mutual Multiple (LCM) and GCF of 36 and 64, i.e. GCF × LCM = 36 × 64.

What are the Methods to Discover GCF of 36 and 64?

There are iii normally used methods to detect the GCF of 36 and 64.

• By Prime Factorization
• By Euclidean Algorithm
• Past Long Segmentation

How to Find the GCF of 36 and 64 past Prime Factorization?

To discover the GCF of 36 and 64, we will find the prime number factorization of the given numbers, i.east. 36 = ii × 2 × three × 3; 64 = ii × 2 × two × 2 × ii × two.
⇒ Since two, ii are common terms in the prime factorization of 36 and 64. Hence, GCF(36, 64) = two × two = iv
☛ What is a Prime Number?

How to Find the GCF of 36 and 64 past Long Sectionalisation Method?

To detect the GCF of 36, 64 using long partition method, 64 is divided by 36. The respective divisor (4) when remainder equals 0 is taken as GCF.

Gcf Of 64 And 36,

Source: https://bryanttretind.blogspot.com/2022/10/gcf-of-36-and-64.html

Posted by: wilkincalice.blogspot.com

Share this post